01. Geometry Concepts
1.1.01. geometry concepts
DESCRIPTION
This exercise is using Grasshopper version 1.0.0007
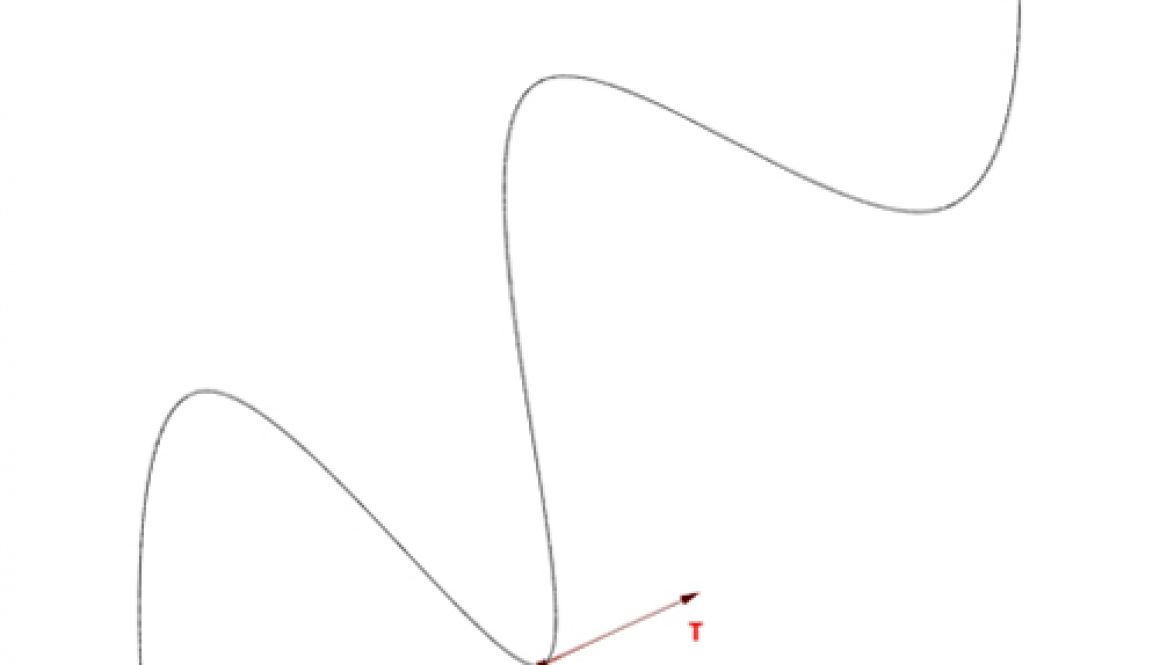
Kristof 1.1. Preface, Introduction
1.1.01. geometry concepts
![]()
DESCRIPTION
This exercise is using Grasshopper version 1.0.0007

Kristof 1.4. Example Exercises, Introduction
1.4.09. image based mesh generation
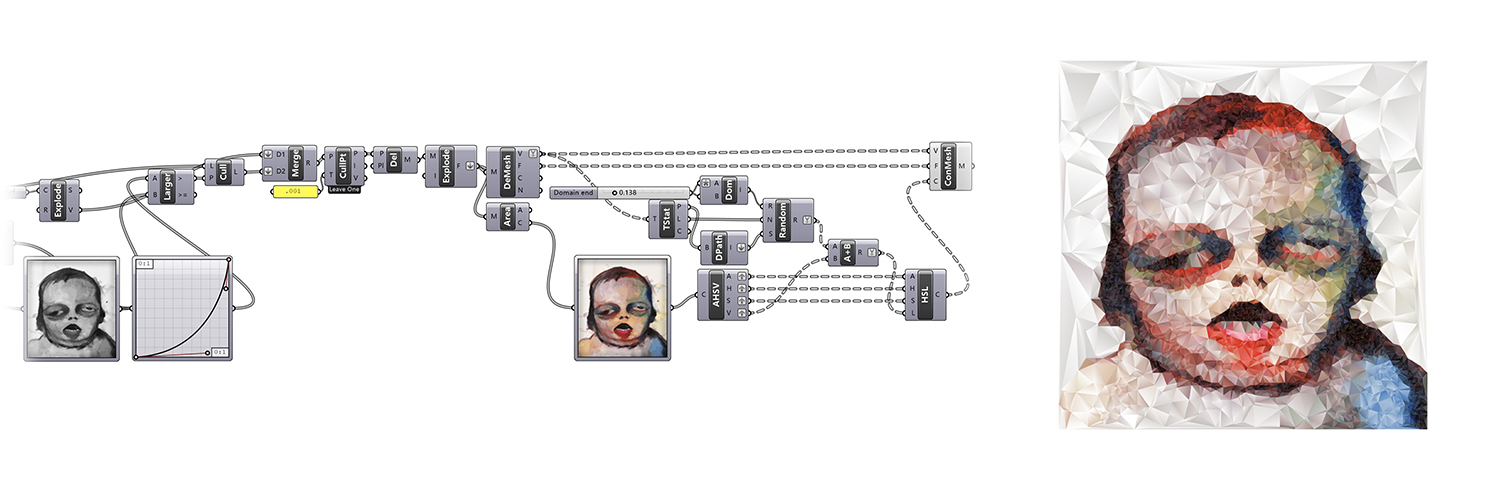
![]()
DESCRIPTION
This exercise shows an image to generate a mesh with varying vertex density based on the image brightness. Each mesh face is then given a colour sampled from the image, but with a random deviation for each face vertex.
This exercise is using Grasshopper version 1.0.0007

Kristof 1.4. Example Exercises, Introduction
1.4.08. blendshaper (for triangulated breps)
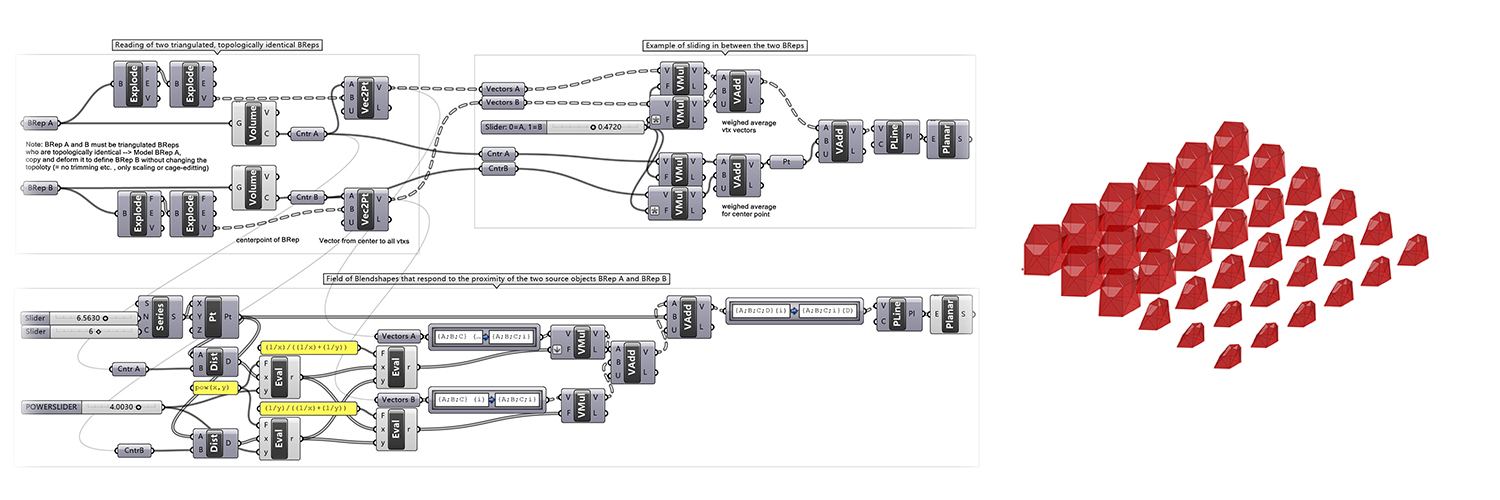
![]()
DESCRIPTION
The Blendshaper blends between two different graphical “expressions” of topologically identical triangulated BReps by morphing between the relative distances of control vertexes to the centre point.
This exercise is using Grasshopper version 1.0.0007
Kristof 1.4. Example Exercises, Introduction
1.4.07. surface panelisation pattern
![]()
DESCRIPTION
This exercise shows how to map a generic pattern onto a surface by systematically connecting a series of numbered surface points. In this example we construct our own hexagonal pattern. The script consists of two parts: what is the pattern a polyline needs to follow once we know the starting point of the hexagon, and which are the starting points of the hexagons. Note that the hexagonal pattern shifts between even and odd rows.
PROCEDURE
1. Define the amount of hexagons in U and V direction
2. Calculate the amount of surface subdivision points needed
3. Calculate the list of indices of the starting points for hexagons
4. From those starting points indices, define the 5 following indices
5. Extract the surface points from the list according to the list of indices
6. Draw a polyline through these points
This exercise is using Grasshopper version 1.0.0007

Kristof 1.4. Example Exercises, Introduction
1.4.06. bitmap surface panelisation
![]()
DESCRIPTION
Panelise a surface based on a bitmap as input. Note that the bitmap can be the real-time outcome of a structural surface analyses or an environmental analysis and thus create a performance-driven procedural setup.
PROCESS
1. Divide an input surface into subsurfaces and find their centerpoint
2. Find the surface normal in the closest point to the center point
3. Multiply the normal vector with a slider that defines the magnitude and direction of the extrusion.
4. Remap the domain of the counterpoints in x-y directions to a 0 to 1 domain (= image domain)
5. Read the brightness value of an image, based on the x-y coordinates. (= similar to mapping the image onto surface).
6. Tweak the brightness values to control the largest and smallest values
7. Use these values to rescale the subsurface contour lines
8. Move the rescaled subsurface contour lines according to the vector from (3)
9. Loft between both curves
This exercise is using Grasshopper version 1.0.0007

Kristof 1.4. Example Exercises, Introduction
1.4.05. 3d pixelator
![]()
DESCRIPTION
This exercise uses the colour values of a random image to define the radii of the circle field. Rather than controlling the domain of the image directly in the Image Sampler button we reparameterise the sample domain by remapping it to a domain from 0 to 1 in both the x and y direction.
PROCESS
1. Define a series of points
2. Remap the arbitrary sampling values to domains from 0 to 1 in both the x and y directions
3.Use the Image Sampler to sample the colour information (values from 0 to 1)
4. Multiply with 255 to RGB values and connect to a shader
5. Use the colour values to define circle diameters for circles on the point grid
6. Preview
This exercise is using Grasshopper version 1.0.0007

Kristof 1.4. Example Exercises, Introduction
1.4.04. IMAGE SAMPLER
![]()
DESCRIPTION
This exercise uses the colour values of a random image to define the radii of the circle field. Rather than controlling the domain of the image directly in the Image Sampler button we reparameterise the sample domain by remapping it to a domain from 0 to 1 in both the x and y direction.
PROCESS
1. Define a series of points
2. Remap the arbitrary sampling values to domains from 0 to 1 in both the x and y directions
3. Use the Image Sampler to sample the colour information (values from 0 to 1)
4. Multiply with 255 to RGB values and connect to a shader
5.Use the colour values to define circle diameters for circles on the point grid
6..Preview
This exercise is using Grasshopper version 1.0.0007
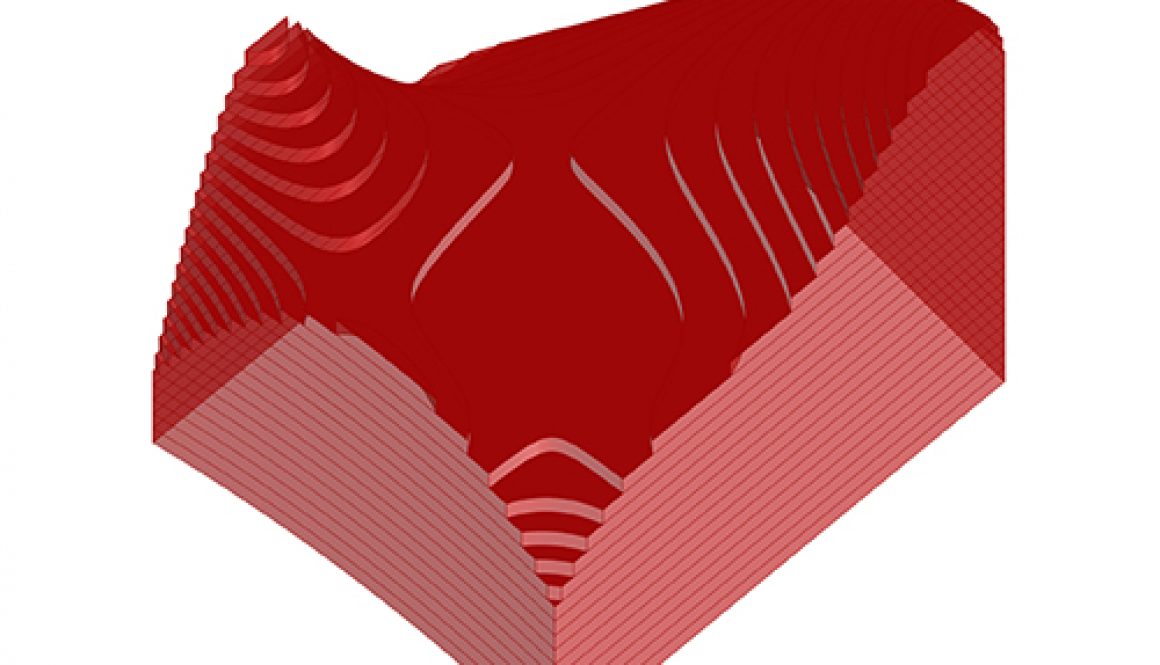
Kristof 1.4. Example Exercises, Introduction
1.4.03. terraced model maker
![]()
DESCRIPTION
Any surface is transformed into a terraced model.
PROCEDURE
1. Define the base plane of a surface’s bounding box
2. Project the surfaces edges onto that base plane
3. Loft the edges with their projection
4. Join the lofted edges with the original surface into one Brep
5. Find the total height of the model and define the amount of wanted terraces
6. Use Pframes to find the section curves with the primary and lofted surfaces
7. Extrude the section curves and use them to create planar surfaces
This exercise is using Grasshopper version 1.0.0007

Kristof 1.4. Example Exercises, Introduction
1.4.02. egg crater
![]()
DESCRIPTION
Egg crate any surface as a first step towards Fabrication.
PROCEDURE
1.Get the bounding box and use the edges
2.Explode this bounding box and use the edges
3.Using a slider to choose which edges to use as a main direction
4.Using a slider for PFrames to distribute orthogonally on the edge
5.Find the intersection between the PFrames and the input Brep
6.Create a planar surfaces from the section lines
This exercise is using Grasshopper version 1.0.0007

Kristof 1.4. Example Exercises, Introduction
1.4.01. eladio dieste wall
![]()
DESCRIPTION
Based on two varying sinusoids, this definition creates a lofted surface between a pre-defined number of connection lines.
PROCEDURE
1. Input Parameters
2. Create a range with the predefined amount of points and the wall length as an end value.
3. Use the graphmapper to define the two base curves
4. Create two rows of points according to the graph curves
5. Connect them with lines
6. Loft between those lines
This exercise is using Grasshopper version 1.0.0007