DESCRIPTION 

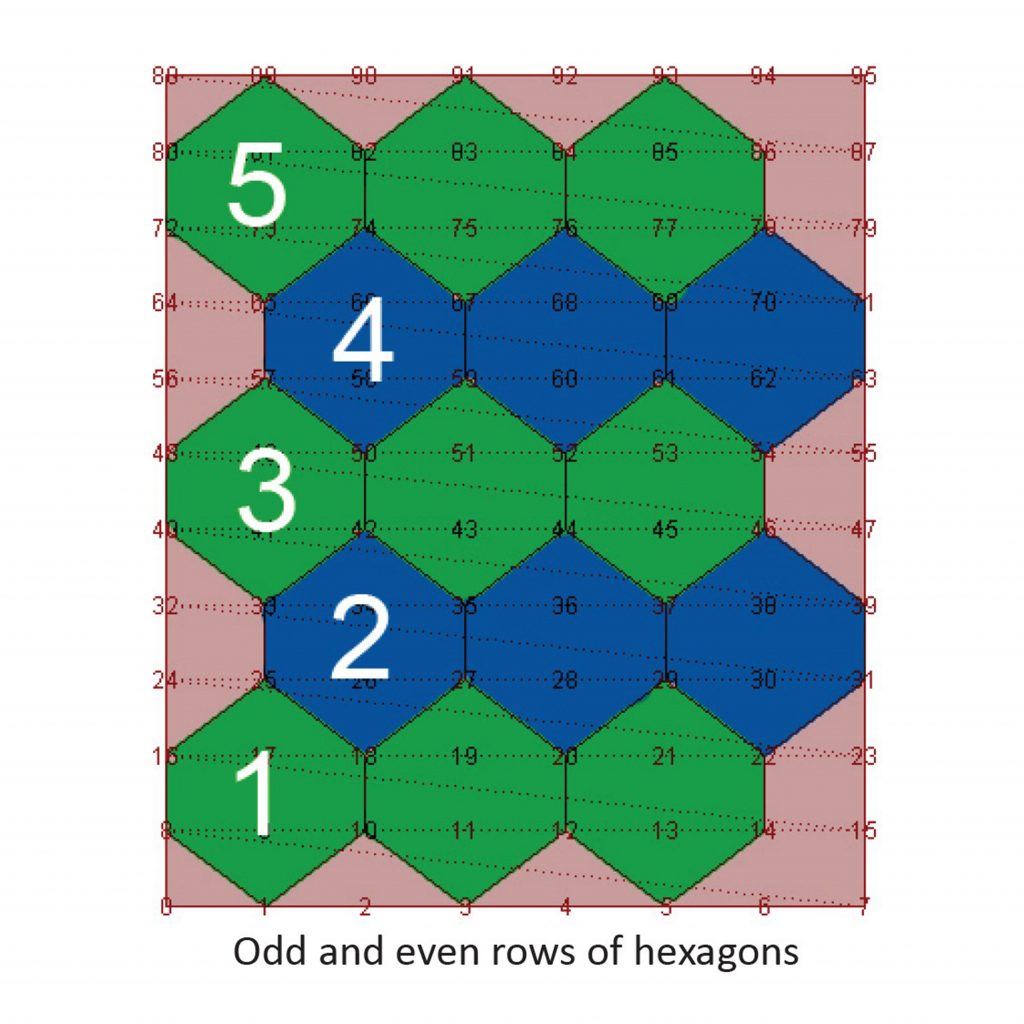
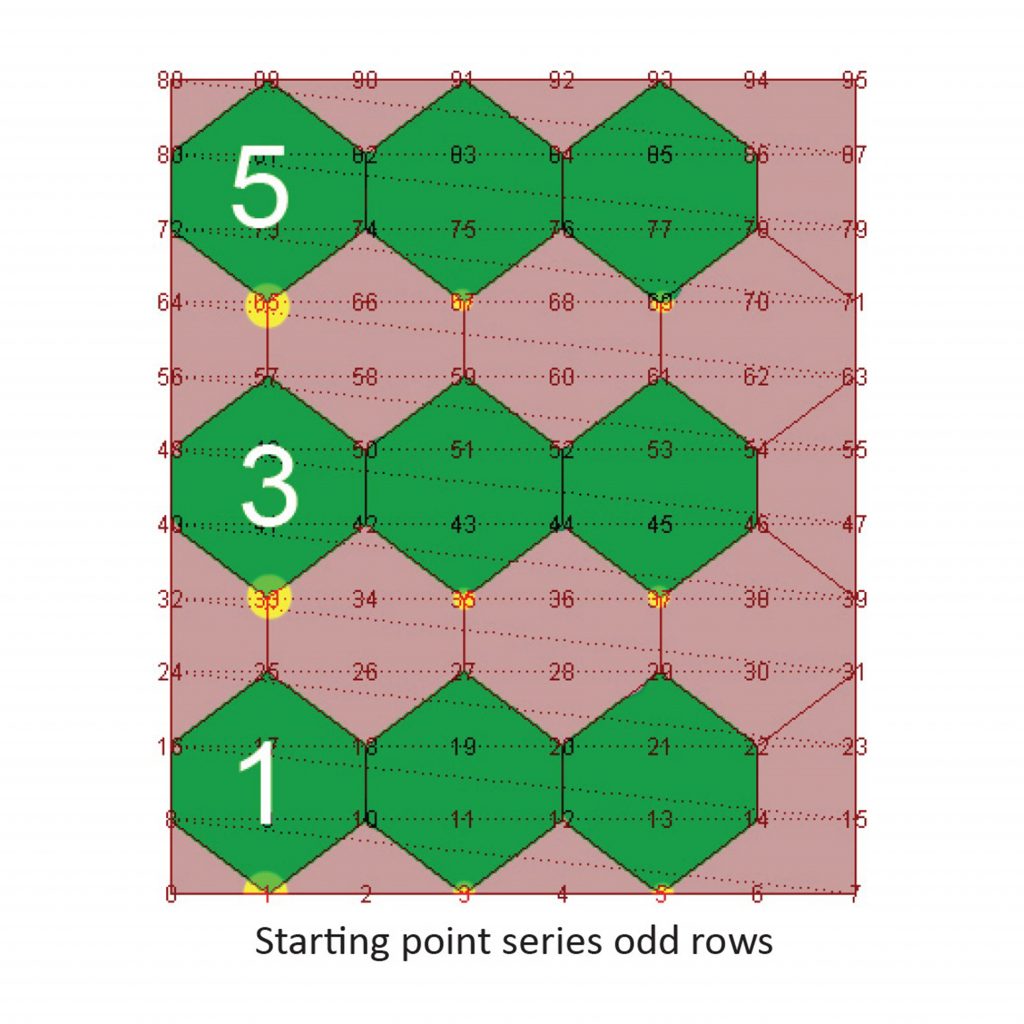
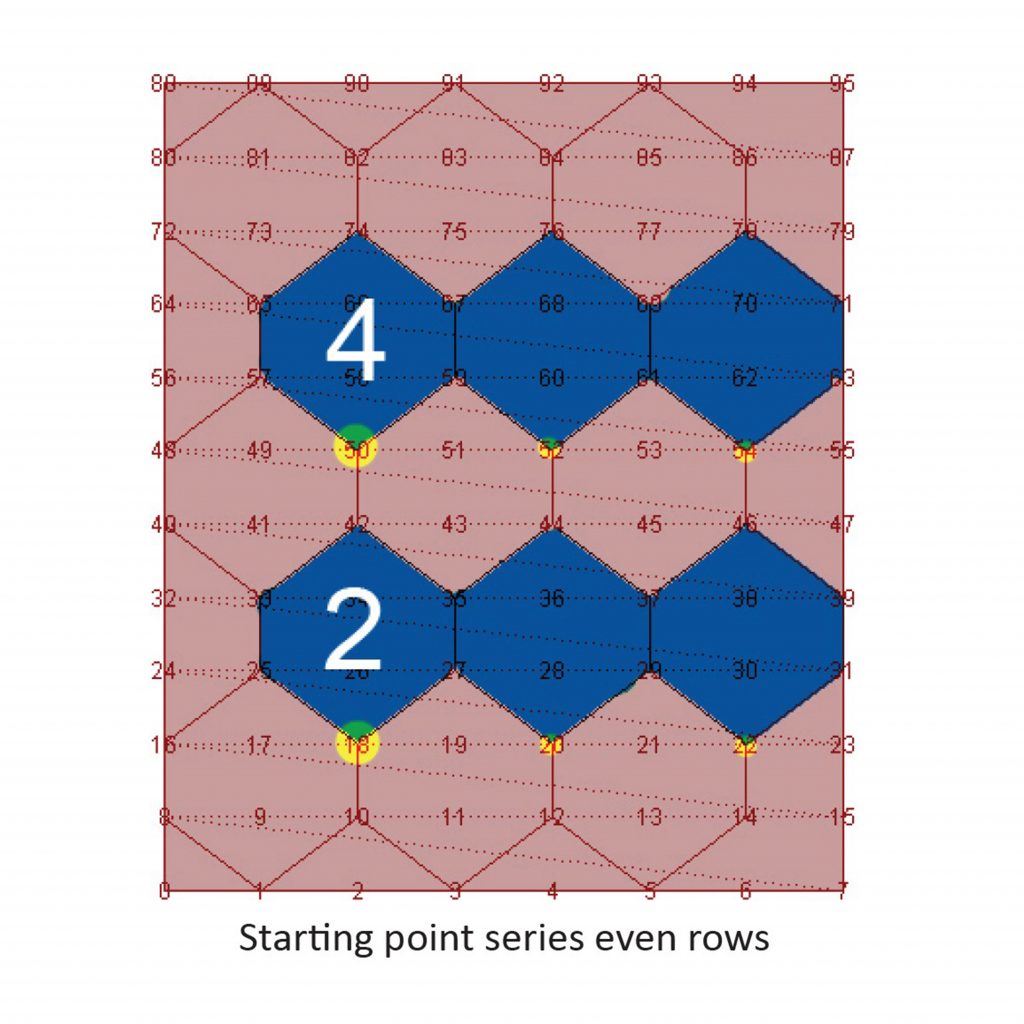
This exercise shows how to map a generic pattern onto a surface by systematically connecting a series of numbered surface points. In this example we construct our own hexagonal pattern. The script consists of two parts: what is the pattern a polyline needs to follow once we know the starting point of the hexagon, and which are the starting points of the hexagons. Note that the hexagonal pattern shifts between even and odd rows. 

PROCEDURE

1. Define the amount of hexagons in U and V direction
2. Calculate the amount of surface subdivision points needed
3. Calculate the list of indices of the starting points for hexagons
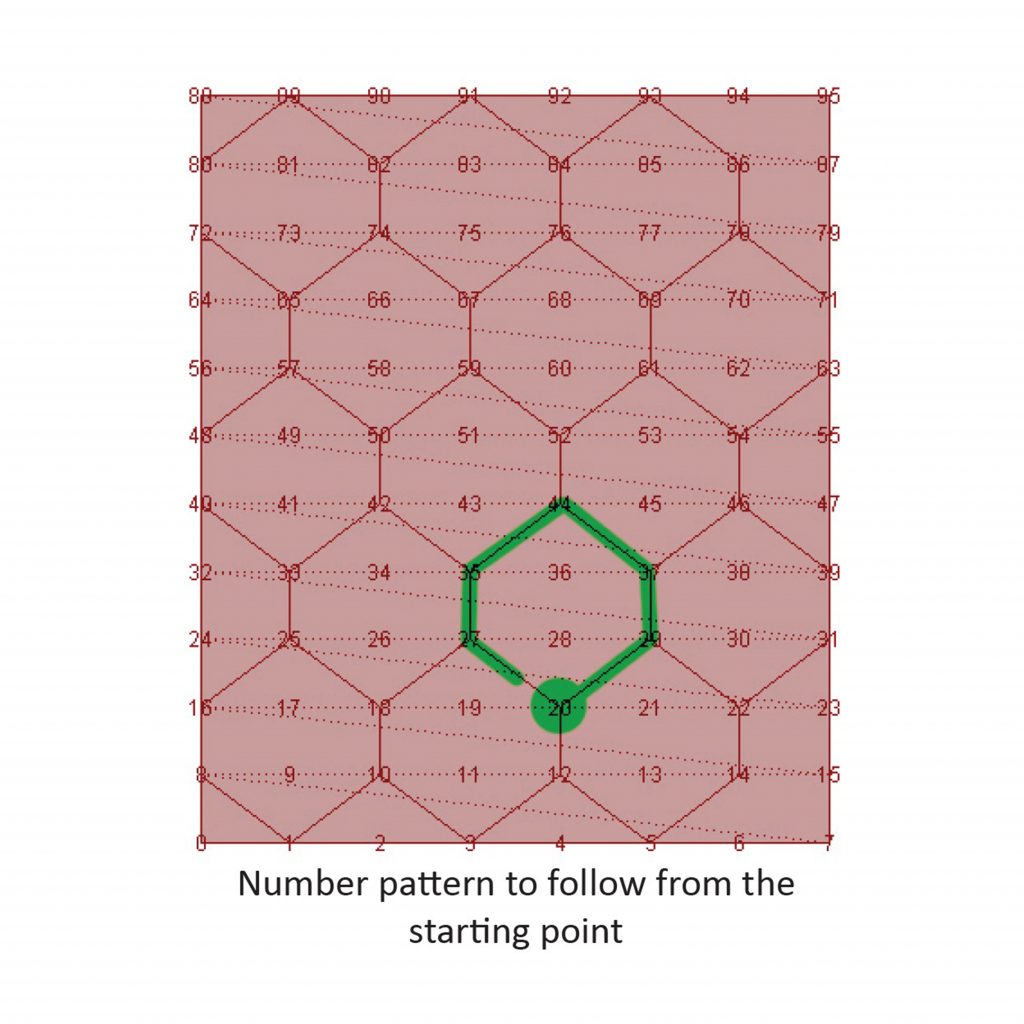
4. From those starting points indices, define the 5 following indices
5. Extract the surface points from the list according to the list of indices
6. Draw a polyline through these points